Tamaño de la muestra y reglas de decisión

Hay que tomar una serie de decisiones cuando se comprueba el acuerdo intercodificadores. Por ejemplo, cuánto material de datos hay que utilizar, cuántas instancias hay que codificar con un código determinado para que el cálculo sea posible y cómo evaluar el coeficiente obtenido.

Tamaño de la muestra

Los datos que utilice para el análisis ICA deben ser representativos de la cantidad total de datos que haya recogido y, por tanto, de aquellos cuya fiabilidad esté en duda. Además, el número de codificaciones por código debe ser suficientemente alto. Como regla general, las codificaciones por código deberían producir al menos cinco acuerdos por azar.

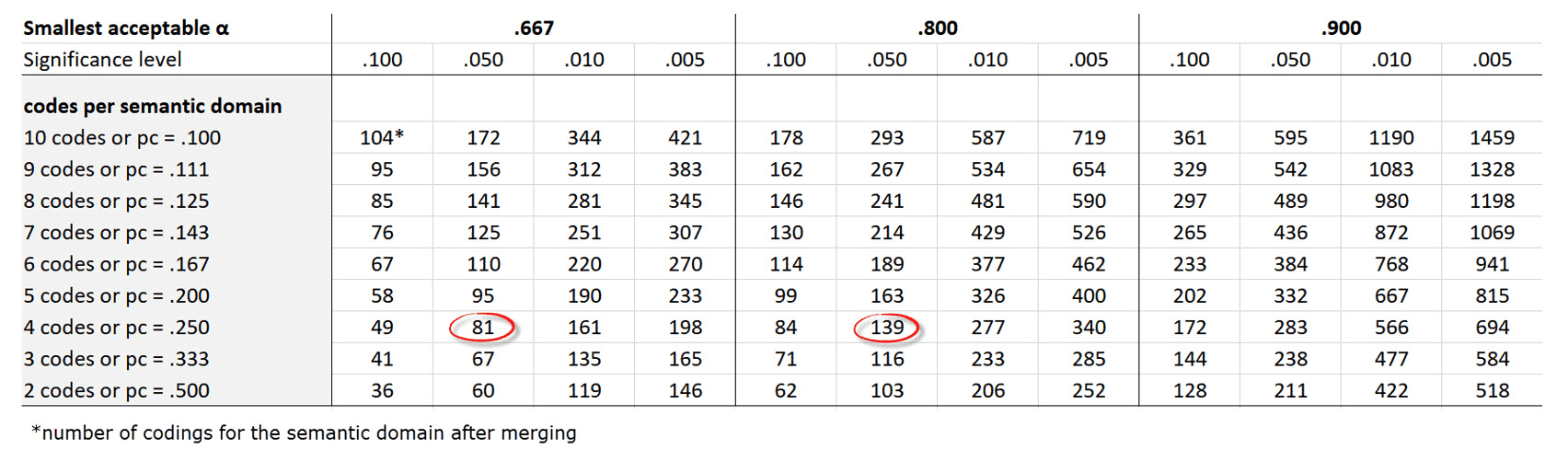
Krippendorff (2019) utiliza la fórmula 3.7 de Bloch y Kraemer (1989:276) para obtener el tamaño de muestra necesario. La siguiente tabla indica el tamaño de la muestra que se necesita cuando se trabaja con dos codificadores.

• las tres menores fiabilidades aceptables α min: 0,667 / 0,800 / 0,900

• para cuatro niveles de significación estadística: 0,100 / 0,050 / 0,010 / 0,005

• para dominios semánticos de hasta 10 códigos (=probabilidad pc):

Ejemplo Si tiene un dominio semántico con 4 códigos y cada uno de los códigos está distribuido de forma equitativa (pc = 1/4 = 0,25), y si el alfa mínimo debe ser de 0,800 a un nivel de significación estadística de 0,05, necesita un mínimo de 139 codificaciones para este dominio semántico. Para un alfa inferior de 0,667, se necesita un mínimo de 81 codificaciones con el mismo nivel de significación estadística.

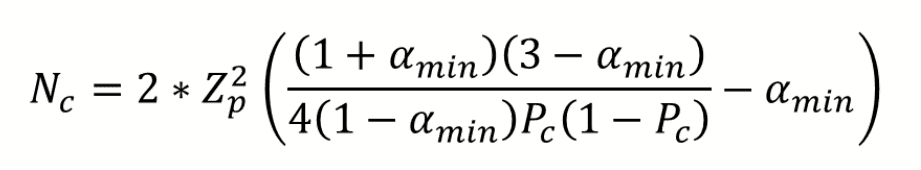
Se aplica a 2 codificadores, y para dominios semánticos hasta 10 subcódigos. Si tiene más de dos codificadores, más de 10 subcódigos en un dominio o una distribución desigual dentro de un dominio, deberá ajustar la ecuación y calcular usted mismo el tamaño de muestra necesario.

• Más de dos codificadores: Es necesario multiplicar Z al cuadrado por el número de codificadores.

• Más de 10 subcódigos por dominio: Hay que ajustar el valor de pc. El valor de pc = 1/número de subcódigos.

• Distribución desigual de las codificaciones dentro de un dominio: Con 4 códigos en un dominio semántico, la proporción estimada pc de todos los valores c en la población es 0,250 (¼); con 5 códigos, es 0,200 (1/5); con 6 códigos, 0,167 (1/6) y así sucesivamente. Si la distribución de sus códigos en un dominio semántico es desigual, tiene que hacer una nueva estimación del tamaño de la muestra utilizando un pc en la fórmula que sea correspondientemente menor que 1/4, 1/5, 1/6 y así sucesivamente.

Nivel aceptable de fiabilidad

La última cuestión a tener en cuenta es cuándo aceptar o rechazar los datos codificados en función del coeficiente ICA. Krippendorff (2019) recomienda:

• Aspire a alcanzar α = 1.000, aunque esto sea solo un ideal.
• No acepte datos con valores de fiabilidad inferiores a α = 0,667.
• En la mayoría de los casos, se puede considerar que un dominio semántico es fiable si α ≥ 0.800.
• Seleccione al menos 0,05 como nivel estadístico de significación para minimizar el riesgo de un error de tipo 1, que consiste en aceptar los datos como fiable si este no es el caso.

El punto de corte que se elija dependerá siempre de los requisitos de validez que se impongan a los resultados de la investigación. Si el resultado de su análisis afecta o incluso pone en peligro la vida de alguien, debe utilizar criterios más estrictos. Un punto de corte de α = 0,800 significa que el 80% de los datos están codificados en un grado mejor que el azar. Si está satisfecho con α = 0,500, esto significa que el 50% de sus datos están codificados en un grado mejor que el azar. Suena un poco como lanzar una moneda y jugar a cara o cruz.