Métodos para evaluar ICA (Acuerdo entre codificadores, por sus siglas en inglés)
An inter-coder agreement coefficient measures the extent to which data can be trusted to represent the phenomena of analytical interest that one hopes to analyze in place of the raw phenomena (Krippendorff, 2019).
ATLAS.ti actualmente ofrece tres métodos para evaluar el acuerdo intercodificadores:
-
Porcentaje de acuerdo simple
-
Índice de Holsti
-
Grupo de coeficientes alfa de Krippendorff
Todos los métodos pueden utilizarse para dos o más codificadores Ya que el porcentaje de acuerdo y el índice de Holsti no tienen en cuenta el acuerdo por azar, recomendamos los coeficientes alfa de Krippendorff para los reportes científicos.
Porcentaje de acuerdo
El porcentaje de acuerdo es la forma más sencilla de medir un acuerdo intercodificadores. Se calcula como el número de veces que un conjunto de valoraciones es igual, dividido por el número total de unidades de observación valoradas, multiplicado por 100.
Las ventajas de la concordancia porcentual son que es sencilla de calcular y puede utilizarse con cualquier tipo de escala de medición. Veamos el siguiente ejemplo: Hay diez segmentos de texto y solo dos codificadores necesarios para decidir si un código aplica o no:
Ejemplo de Codificación con dos codificadores
| Segmentos | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| Codificador 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Codificador 2 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 0 |
1 = acuerdo, 0 = desacuerdo
Así es cómo se calcula
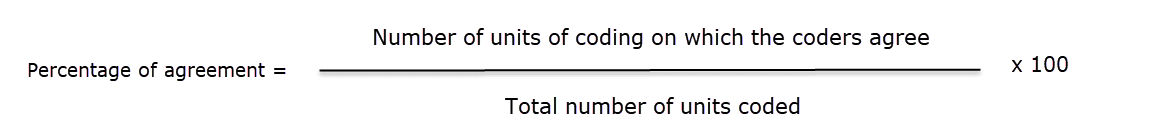
PA = 6 / 10
PA = 0.6 = 60%
El codificador 1 y 2 están de acuerdo en 6 de 10 oportunidades, por lo que el porcentaje de acuerdo es del 60%.
Podría decirse que está muy bien. Sin embargo, este cálculo no tiene en cuenta la concordancia fortuita entre las puntuaciones. Si los dos codificadores no leyeran los datos y se limitaran a codificar aleatoriamente los 10 segmentos, cabría esperar que coincidieran en un determinado porcentaje de las veces sólo por azar. La pregunta es: ¿cuánto mayor es el acuerdo del 60% sobre el acuerdo que se produciría por azar?
El acuerdo que cabe esperar por mera casualidad es del 56% = (9,6 +1,6)/20. Si le interesa el cálculo, eche un vistazo a Krippendorff (2004, p. 224-226). El acuerdo del 60% ahora no parece tan impresionante después de todo. Estadísticamente hablando, el rendimiento de los dos codificadores equivale a haber asignado arbitrariamente 0s y 1s a 9 de los 10 segmentos, y sólo 1 de los 10 segmentos está codificado de forma fiable.
Para calcular el porcentaje de concordancia puede agregar códigos simples en lugar de un dominio semántico, o bien utilizar dominios semánticos reales
Índice de Holsti
El índice de Holsti (Holsti, 1969) es una variación de la medida de porcentaje de acuerdo para situaciones en las que los codificadores no codifican precisamente el mismo segmento de datos. Esto ocurre si los codificadores establecen sus propias citas/. Al igual que el porcentaje de acuerdo,el índice de Holsti no tiene en cuenta el acuerdo por azar.
La fórmula para el Índice de Holsti es:
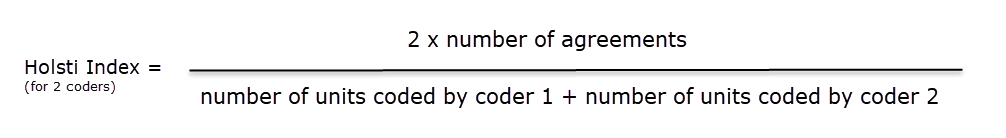
Los resultados del porcentaje de acuerdo y del índice de Holsti son los mismos cuando todos los codificadores codifican los mismos segmentos de datos
Coeficiente Kappa de Cohen
Reconocemos que el Coeficiente Kappa de Cohen es una forma popular de medición, pero hemos optado por no aplicarla debido a las limitaciones que se identifican en los textos al respecto.
"Es bastante desconcertante por qué la kappa de Cohen ha sido tan popular a pesar de tanta controversia con ella. Los investigadores empezaron a plantear problemas con la kappa de Cohen hace más de tres décadas (Kraemer, 1979; Brennan & Prediger, 1981; Maclure & Willett, 1987; Zwick, 1988; Feinstein & Cicchetti, 1990; Cicchetti & Feinstein, 1990; Byrt, Bishop & Carlin, 1993). En una serie de dos artículos, Feinstein & Cicchetti (1990) y Cicchetti & Feinstein (1990) dieron a conocer las siguientes dos paradojas con el kappa de Cohen: (1) Un kappa bajo puede ocurrir con un acuerdo alto; y (2) Las distribuciones marginales desequilibradas producen valores más altos de kappa que las distribuciones marginales más equilibradas. Aunque las dos paradojas no se mencionan en los libros de texto más antiguos (por ejemplo, Agresti, 2002), se introducen plenamente como las limitaciones de kappa en un libro de texto reciente para graduados (Oleckno, 2008). Además de las dos conocidas paradojas mencionadas, Zhao (2011) describe doce paradojas adicionales con kappa y sugiere que kappa de Cohen no es en absoluto una medida general para la fiabilidad entre evaluadores, sino una medida de fiabilidad en condiciones especiales que rara vez se dan. Krippendorff (2004) sugiere que el kappa de Cohen no está cualificado como medida de fiabilidad en el análisis de fiabilidad, ya que su definición de acuerdo casual se deriva de medidas de asociación debido a su suposición de independencia de los calificadores. Argumenta que en el análisis de fiabilidad los calificadores deberían ser intercambiables en lugar de independientes y que la definición de acuerdo de azar debería derivarse de proporciones estimadas como aproximaciones de las proporciones reales en la población de datos de fiabilidad. Krippendorff (2004) demuestra matemáticamente que el desacuerdo esperado de kappa no es una función de proporciones estimadas a partir de datos muestrales, sino una función de las preferencias individuales de dos calificadores para las dos categorías " (Xie, 2013).
Además, el kappa de Cohen solo puede utilizarse para 2 codificadores, y supone un tamaño de muestra infinito. Vea también el artículo en nuestro blog de investigación: Why Cohen's Kappa is not a good choice.
Grupo de coeficientes alfa de Krippendorff
El grupo de coeficientes alfa ofrece varias medidas que permiten realizar cálculos a diferentes niveles. Pueden utilizarse para más de dos codificadores, son sensibles a diferentes tamaños de muestra y pueden utilizarse también con muestras pequeñas.
Alfa binario
A nivel más general, se puede medir si diferentes codificadores identifican las mismas secciones en los datos como relevantes para los temas de interés representados por los códigos Para este análisis se tienen en cuenta todas las unidades de texto, tanto los datos codificados como los no codificados.
Puede, pero no necesita usar dominios semánticos en este nivel. También es posible ingresar un solo código por dominio. Se obtiene un valor para el alfa binario para cada código (o cada dominio semántico) en el análisis, y un valor global para todos los códigos (o todos los dominios) en el análisis.
El valor global del alfa binario podría ser algo que usted quiera publicar en un artículo como valor global para el acuerdo intercodificadores para su proyecto.
Los valores de cada código o dominio semántico proporcionan información sobre qué códigos o dominios son satisfactorios en términos de acuerdo intercodificadores y cuáles son entendidos de forma diferente por los distintos codificadores. Se trata de códigos/dominios que hay que mejorar y probar ganancia, aunque sea con diferentes codificadores.
Si se trabaja con citas predefinidas, el coeficiente binario será 1 para un dominio semántico si solo se han aplicado códigos del mismo dominio semántico, independientemente de qué código dentro del dominio se haya aplicado.
El valor de alfa binario global será siempre 1 cuando se trabaje con citas predefinidas.
cu-alfa
Los coeficientes cu-alfa/Cu-alfa sólo pueden utilizarse en combinación con dominios semánticos. No pueden utilizarse para comprobar la concordancia/descordancia de códigos individuales.
Otra opción es comprobar si diferentes codificadores fueron capaces de distinguir entre los códigos de un dominio semántico. Por ejemplo, si tienes un dominio semántico llamado "tipo de emociones" con los subcódigos:
- emociones::satisfacción
- emociones::entusiasmo
- emociones::vergüenza
- emociones::alivio
El coeficiente indica si los codificadores fueron capaces de distinguir de forma fiable entre, por ejemplo, "satisfacción" y "entusiasmo", o entre "vergüenza" y "alivio”. El cu-alfa le dará un valor para el rendimiento global del dominio semántico. Sin embargo, no le dirá cuál de los subcódigos podría ser problemático. Debe revisar las citas y ver dónde está la confusión.
El coeficiente cu-alfa solo puede calcularse si los códigos de un dominio semántico se han aplicado de forma mutuamente excluyente. Esto significa que solo se aplica uno de los subcódigos por dominio a una cita determinada. Vea también Requisitos para codificar.
Cu-alfa
Cu-alfa es el coeficiente global para todas las cu-alfas. Tiene en cuenta que se pueden asignar códigos de múltiples dominios semánticos a las mismas citas o a las que se superponen. Vea codificación multivaluada. Así, el Cu-alfa no es solo la media de todos los cu-alfas.
Si se han aplicado códigos de un dominio semántico "A" a segmentos de datos codificados con códigos de un dominio semántico "B", esto no afecta al coeficiente cu-alfa ni del dominio A ni del B, pero sí al coeficiente Cu-alfa global.
Puede interpretar el coeficiente Cu-alfa como un indicador del grado de acuerdo de los codificadores sobre la presencia o ausencia de los dominios semánticos en el análisis. Expresado como pregunta: ¿Podían los codificadores identificar con fiabilidad que los segmentos de datos pertenecían a un dominio semántico específico, o los distintos codificadores aplicaban códigos de otros dominios semánticos?
En el cálculo del coeficiente cu- y Cu-alfa, solo se incluyen en el análisis los segmentos de datos codificados.
Calcular el Alfa de Krippendorff
Para una explicación matemática completa sobre cómo se calculan los coeficientes alfa, vea Apéndice ICA.
La fórmula básica para todos los coeficientes alfa de Krippendorff es la siguiente:
alfa = 1 - desacuerdo observado (Do)) / desacuerdo esperado (De)

donde “De” es el desacuerdo por azar esperado.
α = 1 indica perfecta fiabilidad. α = 0 indica ausencia de fiabilidad. Las unidades y los valores que se les asignan no están relacionados estadísticamente. α < 0 cuando los desacuerdos son sistemáticos y superan lo que cabe esperar por azar.
Cuando los codificadores no prestan atención al texto, lo que significa que solo aplican los códigos de forma arbitraria, su codificación no tiene relación con lo que trata el texto, entonces el desacuerdo observado es 1. En otras palabras, el desacuerdo observado (Do) es igual al máximo desacuerdo esperado (De), que es 1. Si ingresamos esto en la fórmula obtenemos:
α= 1 – 1/1 = 0.000.
Si por el contrario, el acuerdo es perfecto, lo que significa que el desacuerdo observado (Do) = 0, entonces obtenemos:
α= 1 – 0 / expected disagreement = 1,000.
Para entender mejor la relación entre el acuerdo real, el observado y el esperado, veamos la siguiente tabla de contingencia:
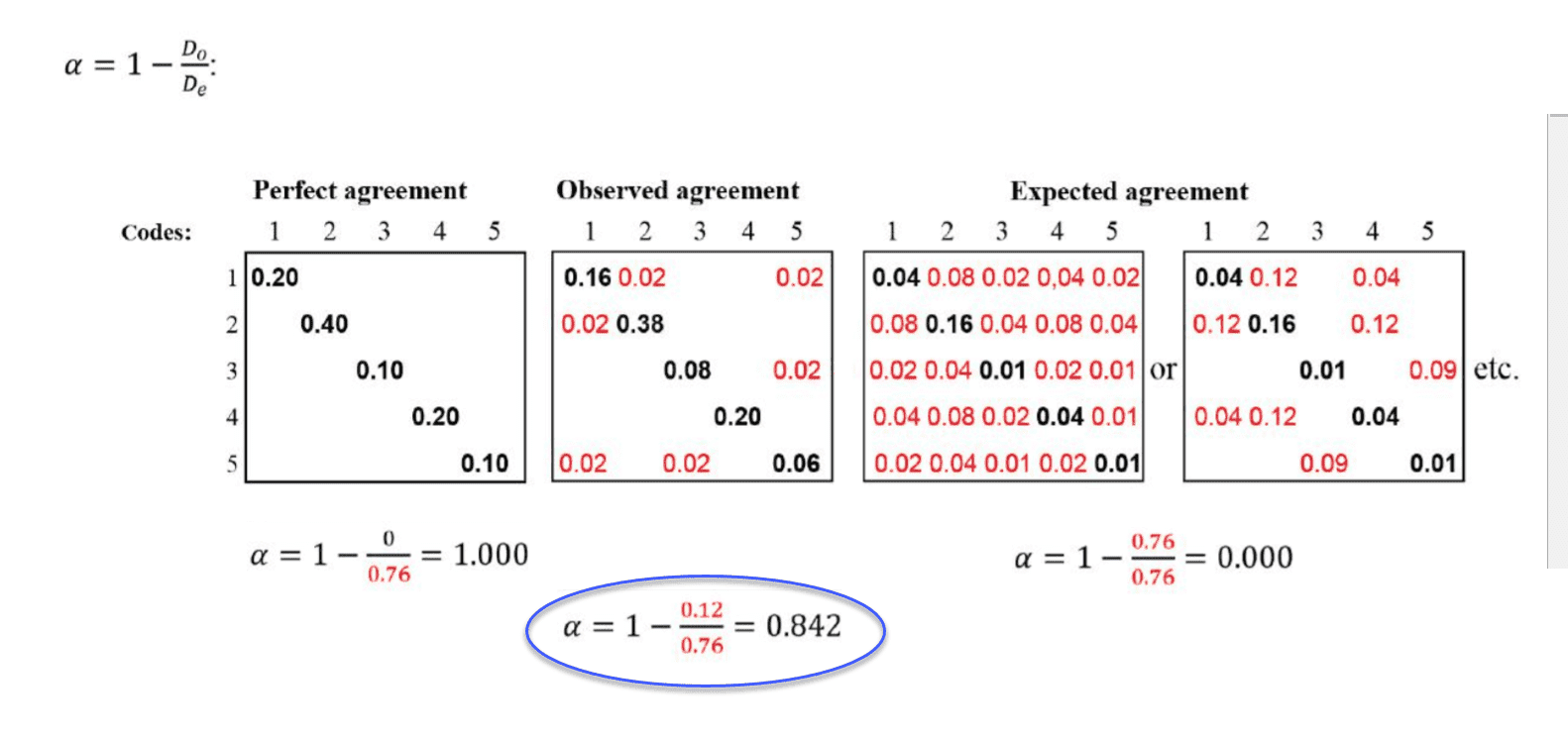
En el ejemplo anterior, las tablas representan un dominio semántico con cinco códigos. Las matrices con el acuerdo/desacuerdo perfecto y esperado sirven como referencia de lo que podría haber sido si el acuerdo fuera perfecto o si los codificadores hubieran aplicado los códigos al azar. Hay dos matrices para el acuerdo/desacuerdo esperado que indican que, desde el punto de vista estadístico, hay muchas posibilidades de atribución aleatoria de los códigos.
Los números negros muestran acuerdo, los números rojos desacuerdo.
En la tabla de contingencia para el acuerdo observado, podemos ver que los codificadores están de acuerdo en asignar el código 4. No hay números rojos, por lo tanto no hay desacuerdo.
Hay algo de desacuerdo sobre aplicar el código 2. El acuerdo es de 38%. En 2% de los casos, se aplicó el código 1 en vez del código 2.
Hay un poco más de confusión sobre aplicar el código 5. Los codificadores también aplicaron el código 1 y el código 3.
Si se tratara de un ejemplo de la vida real, echaría un vistazo a las definiciones de los códigos 5 y 2 y se preguntaría por qué los codificadores tuvieron dificultades para aplicar estos códigos de forma fiable. Sin embargo, el coeficiente es aceptable. Véanse las reglas de decisión. No es necesario repetir la prueba.
Referencias
Banerjee, M., Capozzoli, M., McSweeney, L., Sinha, D. (1999). Beyond kappa: A review of interrater agreement measures. The Canadian Journal of Statistics, Vol. 27 (1), 3-23.
Cohen, Jacob (1960). A coefficient of agreement for nominal scales. Educational and Psychological Measurement. 20 (1): 37–46. doi:10.1177/001316446002000104.
Holsti, O. R. (1969). Content analysis for the social sciences and humanities, Reading, MA: Addison-Wesley.
Krippendorff, Klaus (2004/2012/2018). Content Analysis: An Introduction to Its Methodology. 2ed /3rd /4th edition. Thousand Oaks, CA: Sage.
Zwick, Rebecca (1988). Another look at interrater agreement. Psychological Bulletin, 103, 347-387.
Xie, Q. (2013). ¿De acuerdo o en desacuerdo? A demonstration of an alternative statistic to Cohen's kappa for measuring the extent and reliability of agreement between observer. En Proceedings of the Federal Committee on Statistical Methodology Research Conference, The Council of Professional Associations on Federal Statistics, Washington, DC, USA, 2013.